Kanban-System
Der älteste, aus Japan stammende, Vorschlag zur Implementierung des Pull-Prinzips wird wegen eines speziellen Informationsinstrumentes, der Kanban-Karte, als Kanban-System bezeichnet.
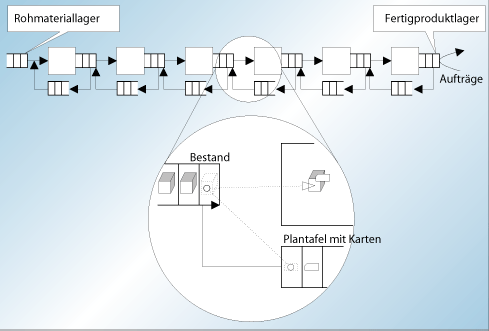
Ein wesentliches Merkmal des Kanban-Systems besteht darin, daß jede Produktionsstufe für jedes dort bearbeitete Erzeugnis bzw. Zwischenprodukt einen eigenen Kanban-Regelkreis besitzt. Im oben dargestellten Bild erkennt man mehrere ($M$) Stationen, hinter denen sich jeweils ein Lagerbereich zur Aufnahme von Behältern mit an der Station fertig bearbeiteten Werkstücken befindet. An jedem Behälter haftet eine (Kanban-)Karte. Auslöser aller Aktivitäten ist das Eintreffen eines Auftrags im Fertigproduktlager (hinter der letzten Station). Ist Lagerbestand vorhanden, dann wird ein Behälter mit Werkstücken aus dem Lager entnommen und die betreffende Karte entfernt und an eine Plantafel geheftet. Sobald die Station $M$ die Bearbeitung eines Behälters abgeschlossen hat, wird geprüft, ob sich eine Karte an der Plantafel befindet und ob ein zu der Karte passender Behälter mit Werkstücken im Lager der vorgelagerten Station $M − 1$ vorhanden ist. Ist dies der Fall, dann wird die an dem Behälter haftende Karte entfernt und an die Plantafel der Station $M − 1$ geheftet. An dem Behälter wird nun die Karte der Station $M$ befestigt und die Bearbeitung kann beginnen. Hat die Station $M − 1$ ihrerseits die Bearbeitung eines Behälters mit Werkstücken abgeschlossen, stellt sie diesen mit der daran haftenden Karte in ihrem Lager ab und prüft, ob an ihrer Plantafel eine Karte vorhanden ist und ob im Lager der Station $M-2$ bereits ein Behälter mit zu der Karte passenden Werkstücken wartet. Dieser Prozeß setzt sich über alle Stationen fort.
Die Leistung eines Kanban-Systems hängt neben den Voraussetzungen [siehe Günther/Tempelmeier(2007)] maßgeblich von der Anzahl von Kanban-Karten ab. Diese begrenzen den Lagerbestand an einer Station. Da die Reduktion von Lagerbestand oft als wichtiges logistisches Ziel angestrebt wird, besteht die Tendenz, die Anzahl der Kanban-Karten so gering wie möglich anzusetzen.
Da die tatsächlichen Durchlaufzeiten der Behälter an einer Station aufgrund verschiedener
Einflüsse (Änderung der Produktionsmengenanteile der zu produzierenden
Erzeugnisse, Variabilität der menschlichen Arbeitsgeschwindigkeit, Maschinenausfälle, Nacharbeit aufgrund von Qualitätsproblemen usw.) zufälligen Schwankungen unterliegen, müssen die Stationen durch eine ausreichende Anzahl von Karten
voneinander entkoppelt werden. In der Praxis (und auch in der beratungsorientierten Managementliteratur) wird die Kartenanzahl einer Produktart
an einer Station durch Multiplikation der erwarteten Durchlaufzeit mit der
mittleren Periodenbedarfsmenge (Behälter pro Periode), erhöht um einen prozentualen
Zuschlag, ermittelt:
$\mathrm{Anzahl Kanbans} = \frac{\mathrm{Bedarf in der Durchlaufzeit + Sicherheitsbestand}}{\mathrm{Behältergröße}}$
Diese Formel wird für jedes Station isoliert angewandt. Die Höhe der Sicherheitsbestands wird willkürlich festgelegt. So wird der Sicherheitsbestand oft als ein Vielfaches des mittleren Periodenbedarfs fixiert. Dies ist sachlich nicht korrekt, da der Sicherheitsbestand nicht vom durchschnittlichen Bedarf, sondern u.a. von der Streuung der Bearbeitungszeiten abhängt. Außerdem gibt es neben den Bearbeitungszeiten noch andere stochastische Einflußgrößen, die einen Sicherheitsbestand erfordern (z.B. Störungen, Blockierungen etc.).
Die "erfahrungsbasierte" Festlegung der Anzahl Karten hat zur Folge, daß praktisch nie die richtige Kartenanzahl verwendet wird. Verfügt eine Station $m$ über zu wenige Karten, dann kann der Fall eintreten, daß sämtliche Karten an Behältern mit fertig bearbeiteten Werkstücken haften, die zum Abruf durch die nachfolgende Produktionsstelle $m+1$ bereitstehen. Wartet nun bereits ein Behälter an der vorgelagerten Station $m−1$ auf Abruf durch die Station $m$, dann könnte diese mit der Bearbeitung beginnen. Da sie aber keine Produktionserlaubnis hat (es befindet sich keine Karte an der Plantafel), ist die Station $m$ blockiert. Die Möglichkeit der Beschränkung des Lagerbestands wird in diesem Fall mit einem Produktionsverlust erkauft. Derartige Blockierungen treten z.B. dann auf, wenn eine nachfolgende Station über einen längeren Zeitraum langsamer oder infolge einer Störung überhaupt nicht arbeitet.
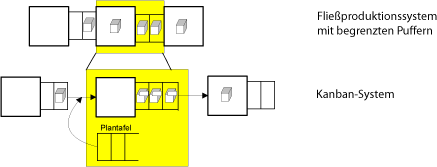
Zur Bestimmung der richtigen Anzahl Karten an den Stationen kann auf eine bestehende Analogie zwischen einem Kanban-System und einem asynchronen Fließproduktionssystem mit beschränkten Puffern zurückgegriffen werden [siehe Gstettner/Kuhn(1996)]. Die Anzahl Karten an einer Station im Kanban-System entspricht der Gesamtanzahl von Werkstücken, die sich in einem asynchronen Fließproduktionssystem an einer Station und dem stromabwärts gelegenen Puffer befinden können. Das folgende Bild zeigt einen Ausschnitt aus einem Kanban-System (unten) und dem entsprechenden Segment eines asynchronen Fließproduktionssystems (oben). An der gelb markierten Station im Kanban-System könnte zwar gearbeitet werden. Da alle drei Karten aber an einem Werkstück heften und die nachfolgende Station noch beschäftigt ist, hat die betrachtete Station keine Produktionserlaubnis und ist unbeschäftigt. Dieser Zustand entspricht der im oben Bildteil dargestellten Situation, in der die äquivalente Station in einem asynchronen Fließproduktionssystem ein Werkstück gerade fertiggestellt hat, dieses aber wegen des beschränkten Pufferplatzes nicht weitergeben kann und demzufolge blockiert ist.
Wegen dieser Äquivalenz kann man zur Analyse eines Kanban-Systems auf Algorithmen zur Leistungsanalyse von Fließproduktionssystemen mit beschränkten Pufferplätzen zurückgreifen. Darüberhinaus kann man zur Bestimmung der optimalen Gesamtanzahl Karten und der optimalen Kartenverteilung auf Verfahren zur Bestimmung optimalen Puffergrößen zurückgreifen. Dies soll anhand eines Beispiel erläutert werden.
Wir betrachten ein Kanban-System mit 10 Stationen. Die Bearbeitungszeiten an allen Stationen sind jeweils mit dem Mittelwert von einer Minute und der Standardabweichung von 0.4 Minuten gamma-verteilt. Es wird eine Produktionsrate von 0.95 Stück pro Minute angestrebt.
Wie groß ist die minimale Anzahl von Kanbans, die für eine gegebene Produktionsrate des Systems benötigt werden, und wie sind diese auf die Stationen zu verteilen?
Nach der obigen Formel würde an jeder Station dieselbe Anzahl von Karten verwendet. Bei einer Bearbeitungszeit bzw. Durchlaufzeit von einer Minute (und einer Behältergröße von 1) würde man unter deterministischen Bedingungen genau eine Karte pro Station einsetzen. Als Sicherheitsbestand könnte man z.B. den Bedarf für 2 Perioden vorsehen, also 2 Karten. Insgesamt hätte man dann pro Station 3 Karten. Allerdings kann mit der obigen Formel nichts darüber ausgesagt werden, ob die Produktionsrate von einem Stück pro Minute dann erreicht wird. Es ist zu vermuten, daß dieses nicht der Fall ist. Jedenfalls sagt die Formel nichts über die erreichbare Produktionsrate aus.
Tatsächlich beträgt die Produktionsrate bei dieser Kartenverteilung nur 0.9141 Stück pro Minute. Die Lagerbestände und die Auslastungsverteilung an den einzelnen Stationen zeigt die folgende Tabelle:
| Station | Karten | arbeitet | leer | blockiert |
|---|---|---|---|---|
1 |
3 |
0.9141 |
-- |
0.0859 |
2 |
3 |
0.9141 |
0.0193 |
0.0666 |
3 |
3 |
0.9141 |
0.0298 |
0.0561 |
4 |
3 |
0.9141 |
0.0367 |
0.0492 |
5 |
3 |
0.9141 |
0.0417 |
0.0442 |
6 |
3 |
0.9141 |
0.0456 |
0.0403 |
7 |
3 |
0.9141 |
0.0505 |
0.0354 |
8 |
3 |
0.9141 |
0.0572 |
0.0287 |
9 |
3 |
0.9141 |
0.0671 |
0.0188 |
10 |
0.9141 |
0.0859 |
-- |
Man sieht, daß es in beträchtlichem Umfang zu Materialmangel und Blockierungen kommt, was letztlich zu Produktionsverlusten führt.
Die optimale Kartenanzahl und -verteilung sieht so aus:
Station |
Karten |
arbeitet |
leer |
blockiert |
|---|---|---|---|---|
1 |
4 |
0.9496 |
-- |
0.0504 |
2 |
5 |
0.9496 |
0.0213 |
0.0291 |
3 |
6 |
0.9496 |
0.0276 |
0.0228 |
4 |
6 |
0.9496 |
0.0268 |
0.0236 |
5 |
6 |
0.9496 |
0.0259 |
0.0245 |
6 |
6 |
0.9496 |
0.0248 |
0.0256 |
7 |
6 |
0.9496 |
0.0239 |
0.0265 |
8 |
5 |
0.9496 |
0.0231 |
0.0273 |
9 |
4 |
0.9496 |
0.0294 |
0.0211 |
10 |
-- |
0.9496 |
0.0504 |
-- |
Die Kartenanzahl an der letzten Station spielt keine Rolle, da angenommen wird, daß das Fertigproduktlager hinter der letzten Station aus der Betrachtung ausgeschlossen ist. Solange mindestens eine Karte vorhanden ist, produziert die letzte Station ohne Blockierungen.
Die Verteilung der Kanbans auf die Stationen wirkt sich nicht nur auf die Produktionsrate, sondern auch auf die Höhe der Lagerbestände zwischen den Stationen eines Fließproduktionssystems aus. Man kann sich auch die Frage stellen, mit wieviel Lagerbestand zu rechnen ist, wenn einen bestimmte Produktionsrate erreicht werden soll. Das folgende Bild zeigt den Zusammenhang zwischen dem Lagerbestand und der Produktionsrate in einem System mit 6 Stationen. (Die Kartenanzahl an der letzten Station wurde weggelassen.) Die Bearbeitungszeiten an allen Stationen sind jeweils mit dem Mittelwert 1 exponentialverteilt.
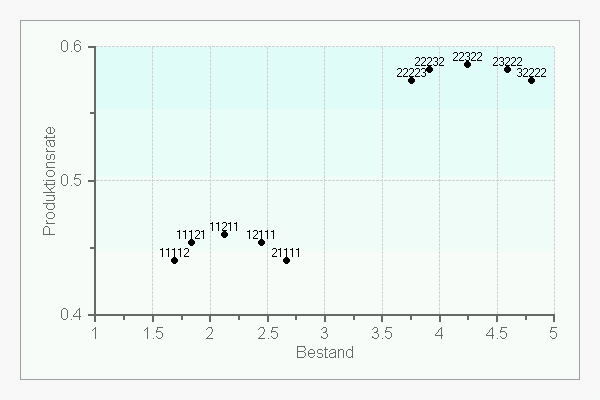
Man erkennt einzelne Gruppen, in denen ausgehend von einer Gleichverteilung der Kartenanzahl jeweils eine weitere Karte alternativ an jeder Station eingefügt worden ist. Es zeigt sich, daß eine gegebene Produktionsrate mit unterschiedlich hohen Lagerbeständen erreicht werden kann, je nachdem, wie die Karten auf die Stationen verteilt werden.
Das folgende Bild verdeutlicht den drastischen Einfluß, den die Anzahl Karten (und ihre Verteilung) auf den Lagerbestand bei nahezu gleichbleibender Produktionsrate haben kann. So erreicht man mit den Kartenverteilungen 22333 und 33322 dieselbe Produktionsrate (0.6121). Im ersten Fall beträgt der Lagerbestand aber 4.1, während er im zweiten Fall nahe bei 6.2 liegt.
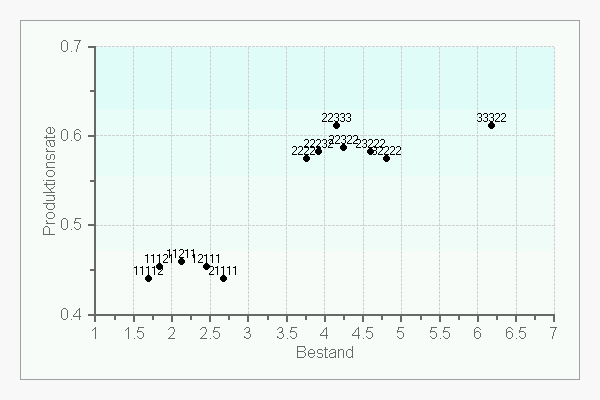
Diese Bilder zeigen deutlich, daß die oben genannte "Daumenregel" zur Bestimmung der Anzahl Karten an den Stationen i.d.R. zu suboptimalen Ergebnissen führen muß.
Siehe auch ...
- Produktions-Management-Trainer
- Analyse längerer Fließproduktionssysteme mit begrenzten Puffern
- CONWIP-System
- Pull-Prinzip
- Push-Prinzip
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Gstettner, S. und H. Kuhn (1996). Analysis of production control systems kanban and CONWIP. International Journal of Production Research, 34, S. 3253-3273 |
