Sicherheitsbestand - Probleme
Immer dann, wenn der Lagerzugang aufgrund von unzuverlässigen Anlieferungen und/oder der Lagerabgang infolge der auftretenden zufälligen Schwankungen der Periodennachfragemengen nicht deterministisch sind, muß das Lager durch Sicherheitsbestand gegen die Unsicherheit im Risikozeitraum geschützt werden. Geschieht das nicht, dann kommt es zu Lieferproblemen bzw. Fehlmengen. Diese wiederum führen dazu, daß die Abnehmer der Produkte - dies können externe Kunden oder andere Mitglieder einer Supply Chain sein - erst nach einer lagerbedingten Wartezeit beliefert werden. Unter bestimmten Annahmen kann der Sicherheitsbestand als ein Vielfaches der Standardabweichung der Nachfragemenge in der Wiederbeschaffungszeit bzw. im Riskozeitraum, dargestellt werden. Dieses Vielfache wird in oft auch als Sicherheitsfaktor bezeichnet.
In der Praxis findet man häufig folgende Vorgehensweisen bei der Festlegung des Sicherheitsbestands:
-
Messung des Sicherheitsbestands in der Dimension "Anzahl durchschnittlicher Periodennachfragemengen" (Bestandsreichweite).
Diese Vorstellung, den Sicherheitsbestand so zu messen, stammt aus der Welt der Finanzanalysten (Lagerumschlagshäufigkeit) und hat mit optimaler Bestandsplanung nichts zu tun. Der Sicherheitsbestand hängt vor allem von der Streuung der Periodennachfragemenge bzw. der Nachfragemenge im Risikozeitraum und nicht von ihrem Mittelwert ab. Wenn man nun den Sicherheitsbestand mit der Vorgabe einer angestrebten Bestandsreichweite festlegt, dann trifft man höchstens durch Zufall den angestrebten Servicegrad. In den meisten Fällen liegt man aber falsch. Das bedeutet: der Servicegrad wird entweder überschritten oder aber unterschritten. Damit sind entweder die Lagerkosten zu hoch oder aber der den Kunden angebotene bzw. zugesagte Servicegrad wird nicht erreicht. Beides ist unerwünscht und vermeidbar.
Ein einfaches Beispiel kann dies verdeutlichen: Wir betrachten eine $(s,q)$-Lagerpolitik für ein Produkt mit stationärem Bedarf und einer erwarteten Periodennachfragemenge von $E\{D\} = 100$ Mengeneinheiten. Die Bestellmenge möge $q = 1000$ Mengeneinheiten betragen. Die Wieder-beschaffungsfrist ist deterministisch bekannt und beträgt ℓ = 8 Perioden. Der Einfachheit halber wird eine kontinuierliche Lagerüberwachung angenommen. Nehmen wir an, der Lagerdisponent legt eine Bestandsreichweite des Sicherheitsbestands von einer Periode fest. Der Sicherheitsbestand beträgt folglich $SB=100$ Mengeneinheiten. Berücksichtigt man die erwartete Nachfragemenge im Risiko-zeitraum (800 Mengeneinheiten), dann ergibt sich ein Bestellpunkt in Höhe von $s=900$ Mengen-einheiten. In Abhängigkeit davon, wie hoch die zufälligen Schwankungen der Periodennachfrage-menge nun sind, und in Abhängigkeit davon, welche Bestellmenge festgelegt worden ist, wird der Lagerdisponent unterschiedliche Servicegrade erreichen. Denn das Kriterium Bestandreichweite greift auf den Erwartungswert der Nachfrage und nicht auf ihre Streuung zurück und berücksichtigt die Höhe der Bestellmenge überhaupt nicht. -
Um das zu veranschaulichen, betrachten wir jetzt folgende Situationen:
-
Die Periodennachfragemenge ist normalverteilt mit einer Standardabweichung $\sigma = 25$. In diesem Fall wird ein $\beta$-Servicegrad von 99.75% erreicht. Bei einer Halbierung der Bestellmenge von $q=500$ wäre der realisierte $\beta$-Servicegrad 99.50%.
-
Nehmen wir jetzt an, die Periodennachfragemenge unterliegt wesentlich höheren stochastischen Schwankungen und ist mit der Standardabweichung von $\sigma = 40$ Mengeneinheiten gamma-verteilt. In diesem Fall ereicht das Lager nur noch einer Servicegrad von $\beta=98.71%$. (Zur detaillierten Berechnung vgl. Tempelmeier (2018a)). Bei einer Bestellmenge von $q=500$ wäre der realisierte $\beta$-Servicegrad nur noch 97.42%.
-
Schließlich sei unterstellt, daß die Periodennachfrage sehr unregelmäßigen Schwankungen unterliegt und daß die Standardabweichung $\sigma = 80$ Mengeneinheiten beträgt, wobei wieder eine Gamma-Verteilung angenommen wird. In diesem Fall ergibt sich bei einem Bestellpunkt $s=900$ ein realisierter $\beta$-Servicegrad von 94.83%. Bei einer Bestellmenge von $q=500$ wäre der realisierte $\beta$-Servicegrad nur noch 89.93%.
Das Beispiel zeigt deutlich, daß der Lagerdisponent bei Verwenung des Kriteriums "Bestandsreichweite" für die Festlegung des Sicherheitsbestands keine Kontrolle über den realisierten $\beta$-Servicegrad hat. Sowohl die Höhe der Bestellmenge als auch die Standardabweichung bzw. Varianz der Nachfragemenge haben einen Einfluß auf den Servicegrad. Der Einfluß der stochastischen Schwankungen der Nachfragemenge auf den realisierten Servicegrad ist darüberhinaus umso größer, je kleiner der verwendete Bestellmenge ist.
Betrachten wir noch einige weitere Ergebnisse. Dabei werden folgende Parameter angenommen:Fall 1 2 3 4 5 6 $q$ 1000 1000 1000 1000 1000 1000 $\ell$ 8 8 8 8 8 8 $\mu$ 100 100 100 100 100 100 $\sigma$ 25 40 25 40 80 80 Für die Fälle 1 bis 4 gehen wir von normalverteilten Periodennachfragemengen aus und für die Fälle 5 und 6 unterstellen wir gamma-verteilte Nachfragemengen, da hier die Streuung der Nachfrage so groß ist, daß eine Normalverteilung wegen der Möglichkeit negativer Nachfragemengen zu fehlerhaften Aussagen führen würde.
-
-
Die folgende Tabelle zeigt, welchen Bestellpunkte $s_{opt}$ bzw. welchen Sicherheitsbestand $SB$ man verwenden muß, wenn man einen angestrebten $\beta$-Servicegrad auch tatsächlich in kontrollierter Weise erreichen will.
Fall 1 2 3 4 5 6 $\beta$ 98% 98% 99% 99% 98% 98% $s_{opt}$ 818.31 864.59 849.92 909.58 1051 1149 $SB$ 18.31 64.59 49.92 109.58 251 349 Bestandsreichweite 0.1831 0.6459 0.4992 1.0958 2.51 3.49 Man erkennt, daß ein angestrebter Servicegrad wohl kaum mit einer ganzzahligen Bestandsreichweite erreicht wird. Die mehr oder weniger willkürliche, auf Erfahrungswerten eines Lagerdisponenten basierende und keinesfalls auf den Erkenntnissen der Lagerhaltungstheorie basierende Festlegung des Sicherheitsbestands führt offensichtlich zu einer unkontrollierten Performance des Lagers und sollte vermieden werden.
-
Festlegung des Sicherheitsbestands als ein Vielfaches des mittleren absoluten Abweichung (MAD).
Die mittlere absolute Abweichung (MAD) wird oft als Ersatz für die Standardabweichung verwendet, da Sie für den Praktiker anschaulicher ist und da sich die MAD für den Fall normalverteilter Nachfrage nur durch einen konstanten Faktor von der Standardabweichung unterscheidet (siehe hierzu: Tempelmeier(2018b)). Allerdings wird dieser Zusammenhang oft ungeprüft für alle Produkte - auch für solche mit nicht normalverteilter Nachfragemenge - unterstellt. Insbesondere bei stark schwankendem Bedarf, der z.B. anstelle mit der Normalverteilung besser durch eine Gamma-Verteilung abgebildet wird, führt dies zu erheblichen Fehlern bei der Berechnung des Sicherheitsbestands. Daraus folgt, daß auch hier der angestrebte Servicegrad verfehlt wird.
Im folgenden Bild wird für zwei Servicegrade gezeigt, welcher Fehler bei der Bestimmung des Sicherheitsbestandes gemacht wird, wenn man diesen wie in der Praxis auf der Basis der mittleren absoluten Abweichung unter der Annahme der Normalverteilung berechnet, wenn aber in Wirklichkeit nicht-normalverteilte Nachfrage vorliegt.
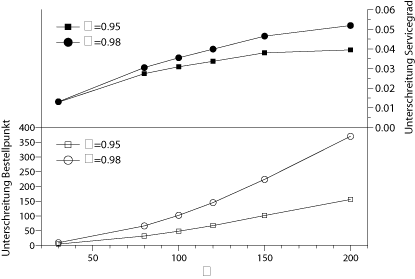
An der x-Achse ist die Standardabweichung der Periodennachfragemenge abgetragen. Im oberen Bildteil sieht man, daß bei einer hohen Standardabweichung $\sigma=200$ und einem angetrebten $\alpha$-Servicegrad von $\alpha=98$% dieser um ca. 5% unterschritten wird. Im unteren Bildteil sieht man, daß in diesem Fall der Bestellpunkt auf der Basis der mittleren absoluten Abweichung um ca. 350 unterschritten würde. Nähere Details zu diesem Beispiel finden sich in Tempelmeier (2018b).
-
Verwendung eines konstanten Sicherheitsbestands trotz dynamischem Nachfrageverlauf .
In vielen Fällen, z.B. in der dynamischen Produktionsplanung und -steuerung, insbesondere auch in der Losgrößen- und Ressourceneinsatzplanung ist die mittlere Periodennachfragemenge eines Produkts nicht stationär, sondern sie unterliegt im Zeitablauf dynamischen Veränderungen. Gerade in mehrstufigen Erzeugnisstrukturen beobachtet man, daß die Losgrößenplanung für ein übergeordnetes (Nachfolger-)Produkt dazu führt, daß der abgeleitete Bedarf für die untergeordneten (Vorgänger-)Produkte dynamisch schwankt. In der Praxis legt man auch für derartige Produkte einen konstanten Sicherheitsbestand unabhängig von der anderen Planungsparametern fest. Dieser Sicherheitsbestand wird in der Losgrößen- und Materialbedarfsplanung bei der Bestimmung des Nettobedarfs berücksichtigt.
Aus der Lagerhaltungstheorie ist weiß man, daß die Bellmenge einen Einfluß auf den Sicherheitsbestand hat. Beispielsweise ist bekannt, daß in einer $(s,q)$-Politik der Bestellpunkt $s$ und damit auch der Sicherheitsbestand mit steigender Bestellmenge $q$ sinkt. Setzt man nun in einem Produktionsplanungs- und -steuerungssystem einen Algorithmus zur Lösung eines dynamisches Losgrößenproblem ein, dann müßte für jedes eingeplante Los ein spezifischer Sicherheitsbestand bestimmt werden. Ein konstanter Sicherheitsbestand hat in diesem Fall keinen Sinn, da unterschiedlich große Lose in unterschiedlichem Umfang Unsicherheit absorbieren.
Unter diesen dynamischen Bedingungen sind zwei Punkte zu berücksichtigen: -
die Wahrscheinlichkeitsverteilung der Nachfrage und
-
die Länge des Risikozeitraums.
Wahrscheinlichkeitsverteilung derNachfrage: Für ein Vorprodukt mit vorwiegend abgeleitetem Bedarf sind die zufälligen Veränderungen der Nachfrage dieses Produkts das Ergebnis der Weiterwälzung von Nachfrageschwankungen der übergeordneten Produkte. Je tiefer das Produkt in der Erzeugnisstruktur angesiedelt ist und je größer seine Verflechtungsbedarfskoeffizienten
in Bezug auf die Endprodukte sind, umso größer sind die Schwankungen der Nach-
fragen des Vorprodukts im Vergleich zu den Bedarfsschwankungen der Endprodukte.
Werden darüberhinaus rüstzeit- oder rüstkostenbedingt mehrere Periodenbedarfe zu Produktionslosen zusammengefaßt, dann kommt es durch die Losbildung zu einer weiteren
Verstärkung der Nachfragevarianz für die untergeordneten Produkte. Werden dagegen große Periodenbedarfsmengen aufgrund knapper Kapazitäten auf mehrere Produktionsperioden verteilt, dann kommt es zu einer Glättung der zufälligen Nachfrageschwankungen. Diese Effekte müssen bei der Festlegung des Sicherheitsbestands berücksichtigt werden.
In der betrieblichen Praxis neigt man dazu, die zufällige Komponente der Periodennachfrage eines Produkts als normalverteilt anzunehmen. Dem herkömmlichen Sukzessivplanungskonzept (MRP-Konzept) folgend wird zunächst auf der Grundlage von prognostizierten Primärbedarfen die Materialbedarfsrechnung durchgeführt. Für die zufällige Komponente des Periodenbedarfs eines untergeordneten Produkts (d.h. den Prognosefehler) wird die Normalverteilung dann i.d.R. ohne weitere Prüfung unterstellt. Dabei wird übersehen, daß die beobachtete Bedarfsentwicklung für ein untergeordnetes Produkt nur teilweise zufallsbedingt ist, zu einem möglicherweise großen Teil aber aus der Produktionsplanung (bzw. Losgrößenplanung) für übergeordnete Produkte resultiert. Die Bestimmung der Wahrscheinlichkeitsverteilung der Nachfrage eines untergeordneten Produkts in einer mehrstufigen Erzeugnisstruktur ist vor allem dann schwierig, wenn in größeren Losen produziert wird. Denn die Losgrößenentscheidungen einer übergeordneten Erzeugnisstufe beeinflussen die zeitliche Struktur der Bedarfsmengen, die im Rahmen der Materialbedarfsrechnung auf die untergeordneten Erzeugnisstufen überwälzt werden.
Risikozeitraum: Die zweite Einflußgröße des Sicherheitsbestands ist die Länge des Risikozeitraums. Zunächst ist zu berücksichtigen, daß im MRP-Konzept die Zeitachse in diskrete Perioden aufgeteilt ist. Alle aus der Lagerhaltungstheorie entlehnten Planungskonzepte, die auf einer kontinuierlichen Zeitachse aufbauen, verursachen daher einen Abbildungsfehler. Die Länge des Risikozeitraums besteht damit aus dem Überwachungsintervall und der Länge der Wiederbeschaffungszeit. Die Wiederbeschaffungszeit ist die Zeitspanne zwischen der Freigabe eines Produktionsauftrags und dem Zeitpunkt, an dem der Lagerzugang erfolgt und die produzierte Menge zur Bedarfsdeckung zur Verfügung steht. Diese Zeitspanne ist nicht identisch mit der geplanten Durchlaufzeit, mit der im
MRP-Konzept gerechnet wird. Letztere wird von einem Planer als ein Vielfaches der Zeitspanne festgelegt, die ein Produktionsauftrag ohne Wartezeiten und Produktionsstörungen mindestens im Produktionsbereich verbringt. Ein Produktionsauftrag wird somit weit vor dem Termin zur Produktion freigegeben, der unter deterministischen Bedingungen spätestzulässig wäre.
Prinzipiell muß man aufgrund der bisherigen Ausführungen feststellen, daß es bei dynamischer Nachfrage und dynamischer Losgrößenplanung i.d.R. nicht sinnvoll ist, einen konstanten Sicherheitsbestand zu verwenden? Wird die Losgröße im Zeitablauf verändert, dann muß sich auch der Sicherheitsbestand ändern.
Eine von der jeweiligen Losgröße abhängige Festlegung des Sicherheitsbestands erreicht man, wenn man die Losgrößen mit einem dynamischen stochastischen Losgrößenmodell bestimmt. In diesem Fall legt man Losgrößen unter Berücksichtigung der Tatsache fest, daß die Nachfrage (oder auch die Produktionsausbeute) Zufallsvariablen sind. Da die Losgrößen dann einen modellintern optimierten
Sicherheitszuschlag enthalten, wird das Konzept des „Sicherheitsbestands“ nicht mehr benötigt. Modelle und Lösungsansätze dieses Typs sind in Tempelmeier (2017) ausführlich beschrieben.
Siehe auch ...
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020). Production Analytics. 6. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020). Analytics im Bestandsmanagement. 7 . Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020). Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |
